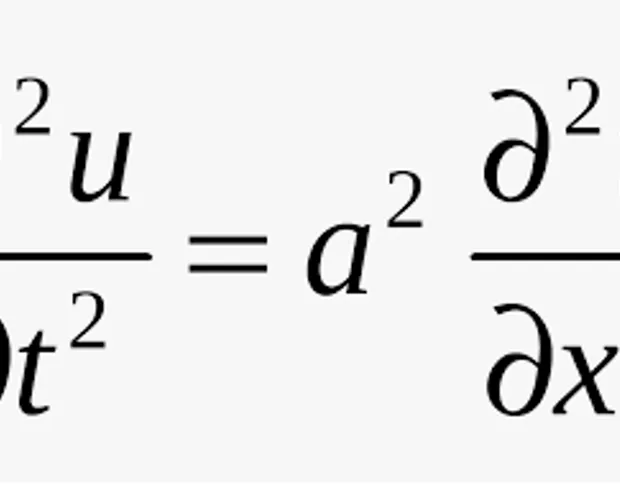
- Кількість кредитів 5
- Тип Вибірковий
- Семестр 5
- Рівень вищої освіти Бакалавр
- Підсумковий контроль Екзамен
Анотація дисципліни: Навчальна дисципліна «Вибрані розділи математичної фізики» є однією з фундаментальних математичних дисциплін і формує важливі навики практичної та наукової діяльності бакалавра спеціальності «Середня освіта (Інформатика)». Знання, набуті студентами з цієї дисципліни, будуть потрібні їм у курсах числових методів, теоретичної фізики, багатьох дисциплінах спеціалізації, які стосуються комп’ютерного моделювання різноманітних явищ і процесів. Вивчення дисципліни ґрунтується на курсах математичного аналізу, лінійної алгебри, аналітичної геометрії, диференціальних рівнянь.
